Are Prediction Markets Reliable? Insights from a Delphi Researcher

Prediction markets can be effective, but they rely on a variety of components, which means they cannot always provide accurate probabilities.

Relying on the assumption of perfect market efficiency in these systems is unrealistic.

In my first article on prediction markets, I broadly explained how prediction markets can serve as a source of truth in complex, uncertain scenarios. I also identified three key biases that hinder specific markets from reaching true probabilities. This second article delves deeper into those three biases: preference bias, hedging bias, and time bias.

Market Efficiency

Market efficiency is crucial for the accuracy of prediction markets. Without it, probabilities will inevitably be skewed.

Take the example of a perfectly efficient market:

• A market is established for a coin toss, and a market maker sells odds of 55c on a heads outcome. This market maker has a 10% advantage per toss since they sell the bet at a 0.55 price while the actual odds are 0.5. Buyers in this market expect to lose 5 cents per coin toss.
• Another market maker enters and offers slightly lower odds at 52.5c. Their advantage drops to 5%, and buyers now expect to lose 2.5 cents per toss.
• A third market maker enters and sets the price at 51c, lowering their advantage to 2%, with buyers only losing 1 cent per toss.

In an efficient market, profit opportunities narrow until they reach the risk premium. For highly predictable events like a coin toss, the risk premium is very low, resulting in a highly efficient market (+/- ~1 basis point).

However, for uncertain outcomes like insurance against wildfires destroying a community, the risk premium is much larger. This requires a greater gap between expected costs and insurance prices to ensure profitability.

Preference Bias

When market efficiency is lacking, prediction markets are prone to biased forecasts (often overestimating probabilities).

People tend to price outcomes higher when they stand to benefit from them. This skews the probability of events occurring (e.g., Chelsea fans are more likely to bet on Chelsea winning the Champions League than Arsenal fans).

The problem arises when inefficient markets fail to correct these biases, and no one steps in to restore prices to the “true” probability.

Let’s look at a real-world example that everyone loves: the U.S. presidential election.

Currently, Polymarket prices Trump at around a 53.6% probability of winning, while Harris is priced at 45.8%.

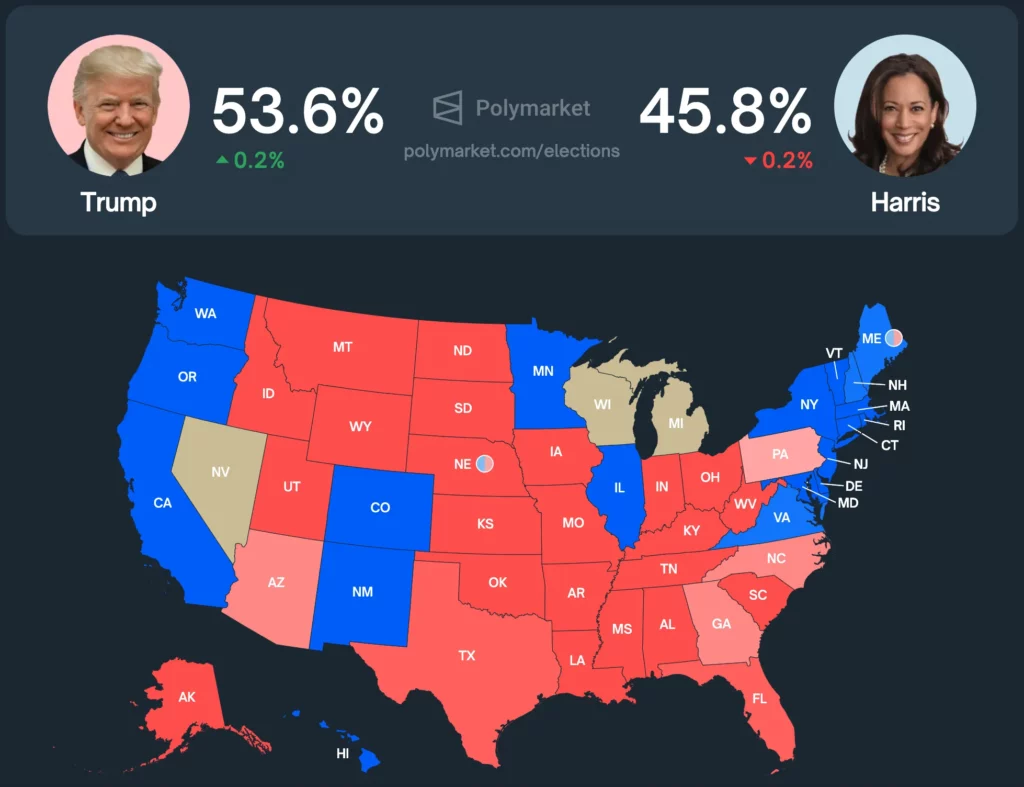
How does this compare to other prediction tools?

• Silver Bulletin: Trump (56.9%) and Harris (42.5%)
• Manifold Markets: Trump (54%) and Harris (43%)
• Metaculus: Trump (55%) and Harris (45%)
• PredictIT: Harris (51%) and Trump (50%)

Polymarket’s core user base consists of crypto users who tend to lean politically right. This is evident, as Polymarket assigns Trump a higher probability of winning than any other prediction tool or market.

Polymarket, which has surpassed $460 million in trading volume for this election, is one of the most liquid prediction markets globally. If any market were to be efficient, it would be this one. However, it still falls short of being fully efficient.

If prediction markets rely on efficiency but can’t revert to true probabilities when biases distort the odds, should they be used as a source of probabilities?

Time Bias

Prediction market efficiency isn’t as simple as the coin toss scenario. If a trader wants to restore a market to true probability, the potential advantage must be worth the effort.

If a market has a 1% upward bias but resolves in six months, the advantage isn’t worth it for someone to hedge, since the annualized return would only be around 2%, lower than the risk-free rate.

The only way to restore the market to true probability is if someone has a counter-interest in the opposing outcome.

As a result, markets won’t reflect efficiency until the bias increases or the time to resolution decreases (thus making it worth a market maker’s while to beat the risk-free rate).

Hedging Bias

Hedging can also distort probabilities in prediction markets by pushing odds higher or lower.

Here’s an example of how hedging manipulates market probabilities:

A trader purchases $1 million worth of SPY EOD call options on the morning of an FOMC meeting. They believe a rate cut will boost SPY, while unchanged rates will push SPY lower. The market currently prices both outcomes at 50:50.

Just before the decision is made, the trader wants to reduce their directional risk but doesn’t want to sell the SPY calls due to lower liquidity. To hedge, they buy $200,000 worth of “NO” positions in the rate change market, pushing the rate cut probability to 48/52.

If market consensus is 50:50, efficiency would dictate that traders buy “YES” shares to restore the market to 50:50. But this doesn’t always happen.

Several factors prevent the market from reverting to the true 50/50 probability:

1. Risk aversion: Traders may not want to take on the directional risk just for a small advantage, especially with infrequent events like FOMC meetings (unlike a repeated coin toss).
2. Information asymmetry: If prediction markets are the sole source of event probabilities, traders may be hesitant to hedge if they suspect the opposing party has access to superior information. This makes arbitraging the market less appealing.

Conclusion

I strongly believe in prediction markets, but using them as the sole source of truth for probabilities is misguided.

They excel at information discovery—I envision prediction markets becoming the go-to platform for real-time odds on any event. However, I disagree with the notion that they are always entirely accurate.

For large events, incorporating error margins into predictions is crucial to account for biases stemming from preference, hedging, or time.